Java [20] – Zadanie: automaty komórkowe, liczby dziesiętne i dwójkowe

Tym razem nieco bardziej złożone zadanie, w którym będzie należało wykorzystać dotychczas zdobyte na kursie umiejętności. Uwaga: nie przewiduję umieszczenia przykładowego rozwiązania tego zadania na stronie.

Automaty komórkowe (ang. Cellular Automata – CA) są systemami składającymi się z „komórek”, które mogą przybierać różne stany a ich los w kolejnych pokoleniach zależy od stanu w jakim znajdowały się w poprzednim pokoleniu oraz stanu sąsiadujących komórek. Za twórcę automatów komórkowych uważa się Johna von Neumanna choć niebagatelny wkład w rozwój koncepcji wniósł także Stanisław Ulam, jeden z przedstawicieli lwowskiej szkoły matematycznej a także współtwórca amerykańskiej bomby wodorowej.
Automat komórkowy zwykle przedstawiany jest jako sieć/plansza podzielona na kwadraty, które odpowiadają poszczególnym komórkom a ich kolor odpowiada poszczególnym stanom. W najprostszej postaci istnieją dwa możliwe stany ukazane za pomocą czerni i bieli interpretowane jako 1 i 0, „włączony” i „wyłączony”, „żywy” i „martwy” itp. W bardziej złożonych systemach stanów może być więcej. System działa przez kolejne „tury” inaczej „pokolenia”, pomiędzy którymi może zmieniać się stan komórek, według określonych reguł.

Automaty jednowymiarowe funkcjonują w komórkach ułożonych w rzędzie. Każda komórka ma zatem dwu sąsiadów. Plansza automatów dwywymiarowych ma zazwyczaj formę „kratki”, więc każda komórka ma 4 lub 8 sąsiadów w zależności od tego czy za sąsiadów uważamy komórki stykające się tylko ścianami czy także kątami. Istnieją także inne warianty, np. plansze składające się z sześciokątów. Najpopularniejszą odmianą dwuwymiarowych automatów komórkowych jest „Gra w życie” (ang. Game of Life) wymyślona przez Johna Conwaya, którą jednak zajmiemy się kiedy indziej.

Do najprostszych automatów komórkowych należą „elementarne automaty komórkowe”, których będzie dotyczyć to zadanie. Należą one do jednowymiarowych automatów komórkowych a więc plansza składa się z jednego szeregu komórek, które mogą przyjmować jeden z dwu stanów. Stan komórki w kolejnym pokoleniu zależy od stanu w jakim znajduje się ona oraz jej dwu sąsiadów w bieżącym pokoleniu. A więc na przykład, można to słownie opisać w ten sposób:
– jeśli komórka jest żywa i jej dwie sąsiadki są żywe, to komórka pozostaje żywa.
– jeśli komórka jest żywa, jej lewa sąsiadka jest żywa a prawa jest martwa, to pozostaje żywa
– jeśli komórka jest martwa a jej dwie sąsiadki są żywe, to staje się żywa
– itd.

Ponieważ istnieje osiem możliwych układów trójek żywych/martwych komórek każdy zestaw reguł opisujących stan komórki w kolejnym pokoleniu musi składać się z tylu zasad. Taki zestaw reguł nazywa się po prostu „regułą”. Każdą regułę można przedstawić graficznie, na przykład tak:

Rząd górny pokazuje wszystkie możliwe układy trójek komórek a dolny, stan komórki środkowej w kolejnym pokoleniu. Powyższa reguła, nazywa się regułą 30. Dlaczego 30?

Ponieważ istnieje 2⁸ możliwych reguł (=256) elementarnych automatów komórkowych, wszystkie reguły mają zwoje numery od 0 do 255 (zob: tu). Numer reguły można łatwo wyliczyć ze znajomości na poszczególnych zasad opisujących los komórki, a robi się to tak:

Pod każdą zasadą umieszczamy 0 lub jeden w zależności od tego czy komórka ma być żywa czy martwa w kolejnym pokoleniu:

Tak otrzymujemy liczbę w systemie dwójkowym, w tym przypadku jest to: 00011110. Teraz pozostaje ją przeliczyć na system dziesiętny. Można to zrobić w ten sposób, że każdej jedynce przyporządkujemy 2 a zeru, zero, kolejne liczby są podniesione do kolejnej potęgi, licząc od prawej do lewej a następnie obliczamy sumę otrzymanych wyrażeń:

0⁷+0⁶+0⁵+2⁴+2³+2²+2¹+0⁰ = 30

Oczywiście, ponieważ 0ⁿ = 0, możemy zignorować elementy z zerami podnoszonymi do potęgi.

Nieco bardziej skomplikowane jest odcyfrowanie poszczególnych zasad z numeru reguły. Musimy oczywiście przeliczyć liczbę w systemie dziesiętnym na dwójkowy. Liczbę, która jest numerem reguły, dzielimy na 2, resztę zapisujemy. Następnie wynik z dzielenia dzielimy znów na 2 itd aż dojdziemy do wyniku z dzielenia mniejszego niż 1.

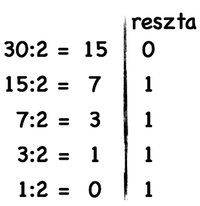
Teraz przepisujemy liczby od dolnej do górnej i otrzymujemy liczbę w systemie dziesiętnym: 11110. Podpisujemy cyfry od prawej do lewej pod poszczególnymi trójkami komórek, uzupełniając brakujące cyfry po lewej zerami. Tam gdzie jest jedynka, komórka w kolejnym pokoleniu powinna być żywa, tam gdzie jest zero, martwa. W konsekwencji otrzymujemy zestaw zasad.

Zauważ, że jeśli komórki czarne zinterpretujemy jako 1 a białe jako 0, to kolejne (od lewej do prawej) trójki komórek na powyższych rysunkach przedstawiają liczby od 0 do 7.

Symulację kolejnych pokoleń można zacząć od pojedynczej żywej komórki w środku rzędu komórek, a kolejne pokolenia przedstawić w kolejnych rzędach. W ten sposób otrzymujemy dwuwymiarowy wzór. Poniżej widać rezultat kilkudziesięciu pokoleń dla reguły 18, która generuje trójkąt Sierpińskiego.

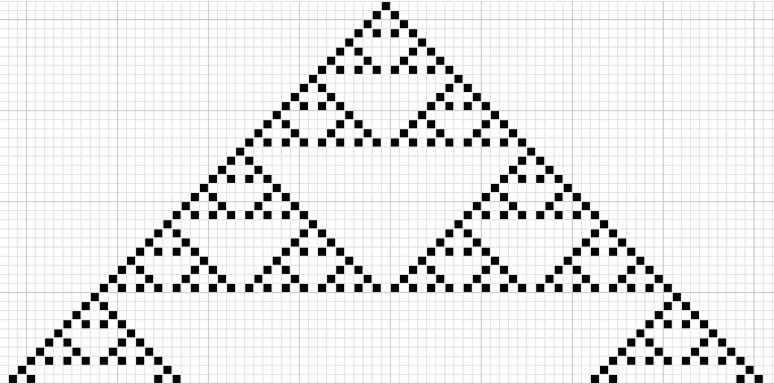
Jeśli przeprowadzamy symulację automatu komórkowego, zazwyczaj plansza ma skończoną liczbę komórek w rzędzie. Należy zatem zastanowić się jak traktować komórki znajdujące się na brzegu. Jedną z możliwości jest uznanie, że za ostatnią komórką po lewej znajduje się pierwsza komórka po prawej (i odwrotnie), plansza w takim przypadku jest „zawinięta”.

Zadanie polega na napisaniu programu, który będzie „rysował” za pomocą znaków (np. #-żywa, .-martwa) kolejne pokolenia jednowymiarowego automatu komórkowego. Użytkownik podaje: liczbę komórek w rzędzie, liczbę pokoleń oraz regułę. Przy czym może podać numer reguły albo poszczególne zasady. W pierwszym przypadku program wypisuje regułę w formie pseudograficznej. W drugim program schematycznie wypisuje kolejne trójki komórek a użytkownik podaje stan środkowej komórki w kolejnym pokoleniu a potem zostaje wypisany numer reguły. Użytkownik może także zdefiniować własne znaki odpowiadające żywym i martwym komórkom a także początkowy układ żywych i martwych komórek, przy czym domyślnie powinna to być jedna żywa komórka po środku planszy. Dodaj także możliwość losowego początkowego układu żywych i martwych komórek, z podanym, przez użytkownika prawdopodobieństwem wystąpienia żywej komórki. Można oczywiście także dodać własne dodatkowe opcje.